Apreciado trader,
Aunque puede ser un concepto muy básico, creo que es muy importante tener claro qué es la volatilidad. Por esta razón, en este artículo vamos a tratar 7 maneras de calcular la volatilidad de un activo. La explicación más sencilla es:
La volatilidad es la medida de lo que cambia el precio de un valor (acción, divisa, etc.) durante un tiempo determinado.
Y ahora os podríais preguntar, ¿y en qué me puede ayudar a mí? Pues muchos inversores lo ven como una medida de riesgo, cuanto mayor sea la volatilidad de una cotización mayor será el riesgo que corro si invierto en ella. También sirve para identificar posibles tendencias emergentes, ya que un aumento en el precio puede indicar una aceleración de la tendencia actual. Un caso más en el que puede ayudar es para el establecimiento de una especie de stop loss en los casos en los que suba mucho el precio de una cotización debido a una noticia o un acontecimiento que influya en su precio.
Un ejemplo muy claro de un activo con mucha volatilidad lo vemos en el Bitcoin, que su precio puede cambiar muchísimo en poco tiempo y eso puede hacer que si inviertes en él tengas que estar muy atento a todo lo que pueda rodear a este valor, debido a que puede cambiar muy rápido. Otras acciones menos volátiles hacen que no tengas que estar tan atento y puedas tener un poco más de calma con tus operaciones. Operar este tipo de activos depende un poco de cómo sea tu perfil de trader y si te gustan las emociones fuertes.
Ya seas de los que le gusten las emociones fuertes o no, vamos a ver como calcular la volatilidad de una acción de diferente formas, para que podáis escoger la que mejor se adapte a vuestro perfil. Vamos a analizar las siguientes:
Tabla de contenidos
Preparando el entorno para calcular la volatilidad
Las librerías que vamos a necesitar para hacer las pruebas son muy simples, e incluso podríamos decir que son las típicas:
import yfinance as yf import pandas as pd import numpy as np
Para hacer las pruebas de cálculos de las volatilidades vamos a hacerlo con el precio de Apple desde 2018 hasta ahora. Así que utilizaremos la librería “yfinance” que nos lo pone muy fácil y que ya hemos cargado antes:
TICKER = "AAPL" data = yf.download(TICKER, start="2018-01-01")
Para el cálculo de todas las fórmulas siempre lo haremos en un periodo de 14, ya que este suele ser el valor que se toma siempre referencia para la mayor parte de los cálculos relacionados con estos indicadores. De todas formas esto es muy adaptable (como en cualquier otro indicador), y podéis cambiarle el valor e ir jugando para encontrar el que más se ajuste a vuestro perfil. Pero, como hemos dicho, por ahora nosotros vamos a ajustarlo a 14.
periodo = 14
Y con esto ya lo tenemos todo listo para empezar a examinar las distintas formas de calcular la volatilidad.
Desviación estándar
Empezamos por la más sencilla y seguramente la que más conozcamos, la desviación estándar. Con esta fórmula calcularemos el precio medio de una acción, y de ahí sabremos lo que se suelen desviar los precios sobre ese precio medio, cuanto más alto sea el valor, mayor será la volatilidad de esta acción.
Vamos a hacerlo con la acción de Apple:
data['returns'] = data['Close'].pct_change() data['Desviacion_estandar'] = data['returns'].rolling(window=periodo).std()
Si ejecutamos este código veremos que el valor que nos devuelve es sobre el que se suele mover el precio de Apple:
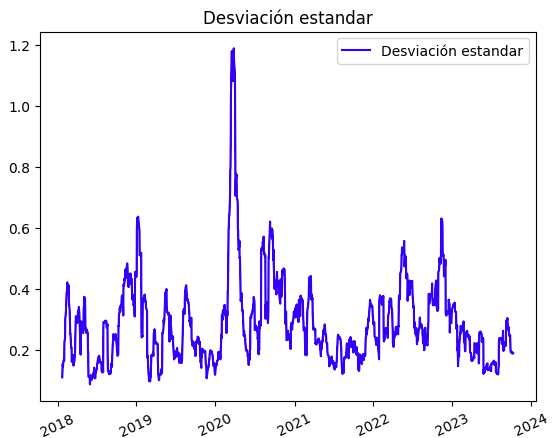
Aunque, como hemos visto, este indicador es muy sencillo, nos detecta muy bien cuando hubo muchísima volatilidad, como por ejemplo en 2020 por la crisis del Covid-19. Esto nos demuestra que no es necesario hacer grandes cálculos para llegar a controlar este valor, sino que con uno sencillo ya funciona lo bastante bien para detectar grandes movimientos.
Average True Range
El Average True Range (ATR) es un indicador de análisis técnico que fue desarrollado por J. Welles Wilder en la década de los 70.
Este indicador fue diseñado con el objetivo de medir la volatilidad actual del precio de un activo, y para lograr este objetivo se centra en la magnitud de los movimientos del precio. El indicador ATR se ha convertido en una herramienta indispensable para los traders que desean evaluar el riesgo de una operación antes de entrar debido a su facilidad de cálculo y a la fama que ha cogido para detectar la volatilidad.
El cálculo del ATR se basa en el cálculo del “Valor verdadero” y esto se hace de la siguiente forma:
- Se calcula la diferencia entre el máximo y el mínimo del día actual.
- Se mide la diferencia entre el máximo del día actual y el cierre del día anterior
- Y por último se calcula la diferencia entre el mínimo del día actual y el cierre del día anterior.
Una vez que se tienen estas tres variables, simplemente se coge el máximo valor de entre las tres. Con el máximo ya conseguido, utilizamos una media móvil exponencial del valor verdadero, con el periodo que hemos elegido, que en nuestro caso es de 14, y con ello ya hemos conseguido el ATR.
El código para calcularlo es el siguiente:
data["High-Low"] = data["High"] - data["Low"] data["High-PrevClose"] = abs(data["High"] - data["Close"].shift(1)) data["Low-PrevClose"] = abs(data["Low"] - data["Close"].shift(1)) data["TR"] = data[["High-Low", "High-PrevClose", "Low-PrevClose"]].max(axis=1) data["ATR"] = data["TR"].rolling(14).mean()
Tendríamos una salida como esta:
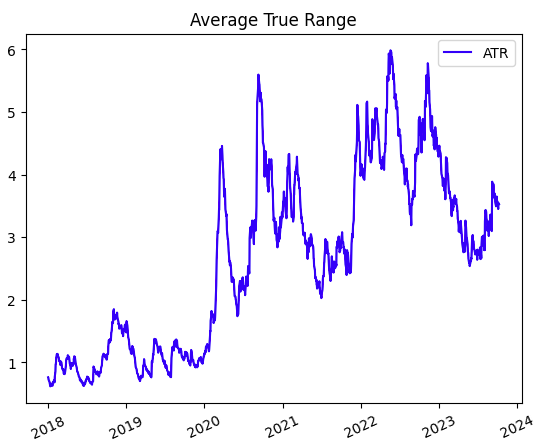
Al igual que pasaba con la desviación estándar, cuanto mayor sea el valor que nos devuelve el indicador ATR mayor será la volatilidad y, lógicamente, si el número es más bajo, el cambio del precio de la acción que se está analizando será menor.
Volatilidad de Parkinson
Esta forma de medir la volatilidad fue desarrollada por el economista estadounidense Michael Parkinson en 1980. En su paper “The Extreme Value Method for Estimating the Variance of the Rate of Return”, Parkinson se basa en la idea de que la volatilidad se relaciona con la amplitud de los movimientos extremos de precio, independientemente de la dirección de esos movimientos. Por esta razón, este indicador utiliza los precios máximos y mínimos en lugar de los precios de cierre. Esto significa que es menos sensible a las fluctuaciones rápidas del mercado y que puede ser más preciso mostrando una volatilidad real, y no por un pico puntual en un precio.
Este indicador se suele utilizar mucho en las situaciones en las que se desee tener en cuenta la amplitud de los movimientos en los precios en una acción, sin tener en cuenta la dirección.
La fórmula para calcular la Volatilidad de Parkinson es la siguiente:
Donde:
- N es el periodo.
- Hi es el precio máximo (high) en el período i.
- Li es el precio mínimo (low) en el período i.
Su implementación en Python será la siguiente:
parkinson_volatility = []
for i in range(periodo, len(data)):
subset = data.iloc[i - periodo:i]
high = subset['High']
low = subset['Low']
parkinson_volatility.append(np.sqrt((1 / (4 * 14)) * np.sum(np.log(subset['High'] / subset['Low']) ** 2)))
data['Parkinson_Volatility'] = [None] * periodo + parkinson_volatility
Si mostramos una gráfica con todos los valores sería algo así:
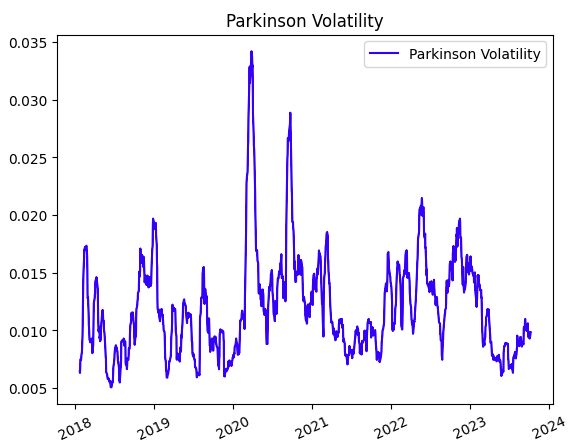
Los inversores pueden utilizar este indicador para determinar el tamaño de sus posiciones en función de los cambios de precio actuales del mercado. Cuando la Volatilidad de Parkinson es alta, sugiere que el riesgo es mayor, por lo que es posible que desees reducir el tamaño de tu posición para gestionar el riesgo.
Chande Momentum Oscillator (CMO)
Este indicador, como su nombre indica, se utiliza para medir el impulso (momentum) de una acción. Su creador fue Tushar Chande, y para hacerlo se basó en la idea de que identificar un impulso puede ayudar a diferenciar posibles puntos de reversión de continuación de una tendencia.
El CMO calcula la diferencia entre la suma de los incrementos de precio y la suma de las bajadas de precio durante un período de tiempo específico (igual que con el ATR nosotros lo haremos con 14 periodos). Luego, este valor se normaliza para producir un indicador oscilante que fluctúa alrededor de cero.
La fórmula del CMO es la siguiente:
Donde:
- SU es la suma de los incrementos de precio durante un período (por ejemplo, cierres más altos que los cierres anteriores).
- SD es la suma de las reducciones de precio durante el mismo período (por ejemplo, cierres más bajos que los cierres anteriores).
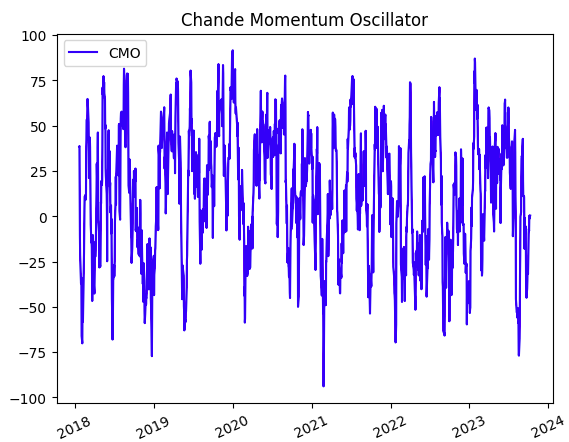
Si el CMO está por encima de cero, sugiere un impulso alcista, mientras que si está por debajo de cero, sugiere un impulso bajista.
data["UP"] = data["Cambio"].apply(lambda x: x if x > 0 else 0) data["DOWN"] = data["Cambio"].apply(lambda x: -x if x < 0 else 0) data["SU"] = data["UP"].rolling(window=14).sum() data["SD"] = data["DOWN"].rolling(window=14).sum() data["CMO"] = ((data["SU"] - data["SD"]) / (data["SU"] + data["SD"])) * 100
Y el resultado sería similar a este:
Volatilidad de Garman-Klass
El Índice de Volatilidad de Garman-Klass fue desarrollado por Richard R. Garman y Robert J. Klass y se basa en el cálculo de la variabilidad de los precios del activo a lo largo del tiempo. Este indicador es una extensión del indicador Parkinson, e incorpora los precios de open, high, low, y close, mientras que el indicador Parkinson no tiene en cuenta ni el precio de apertura ni de cierre. Por esta razón se suele decir que este indicador es más eficaz que la fórmula básica de Parkinson.
La fórmula matemática del índice de Volatilidad de Garman-Klass se basa en la idea de calcularla como la raíz cuadrada de la varianza de los logaritmos naturales de los precios de los días de ganancia y de pérdidas. Y es así:
La implementación en Python de la fórmula es la siguiente:
garman_klass_volatility = []
for i in range(periodo, len(data)):
subset = data.iloc[i - periodo:i]
log_hl = np.log(subset['High'] / subset['Low'])
log_cc = np.log(subset['Close'] / subset['Open'])
ans = 0.5*log_hl**2 - (2*np.log(2)-1) * log_cc**2
garman_klass_volatility.append(np.sqrt(np.sum(ans)*1/periodo))
data['Garman_Klass_Volatility'] = [np.nan] * periodo + garman_klass_volatility
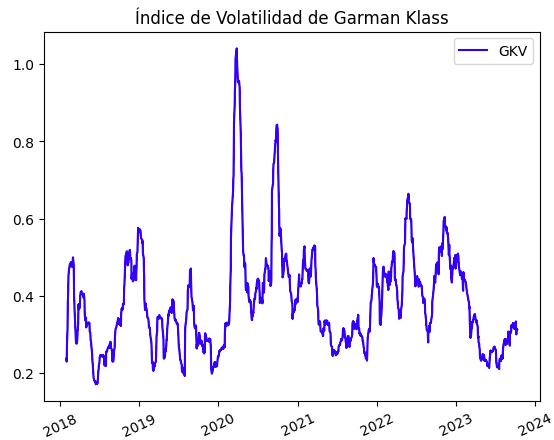
Y la gráfica de la volatilidad de Apple con Garman-klass es:
Close-to-Close Historical Volatility (CCHV)
El Close-to-Close Historical Volatility (CCHV) es otra de las posibles formas de mirar la volatilidad en de una acción. El cálculo del CCHV es relativamente sencillo y se basa en la diferencia entre los precios de cierre de un activo en días consecutivos. El que esta fórmula solamente utilice solamente los precios de cierre a cierre,hace que también sea una forma un poco básica y menos precisa de calcular la volatilidad. Como ya hemos visto, existen otras formas de medir este valor que toman en cuenta más factores además del precio de cierre y que serán más finos a la hora de detectar cambios en una acción.
Vamos a ver la fórmula:
Donde:
- N es el periodo
- ri es el retorno del día i
- r es la media
Una vez que calculas el CCHV, puedes interpretarlo de la siguiente manera: un valor de CCHV más alto indica una mayor volatilidad en el activo, mientras que un número de CCHV más bajo sugiere una menor variación en el precio.
El código para este indicador también es muy sencillo y sería así:
close_to_close_volatility = []
for i in range(periodo, len(data)):
subset = data.iloc[i - periodo:i]
close_prices = subset['Close']
log_returns = close_prices.pct_change().dropna()
close_to_close_volatility.append(np.sqrt((1 / (periodo-1)) * np.sum((subset['Close'][-1]-subset.std())**2)))
data['Close_To_Close_Volatility'] = [None] * periodo + close_to_close_volatility
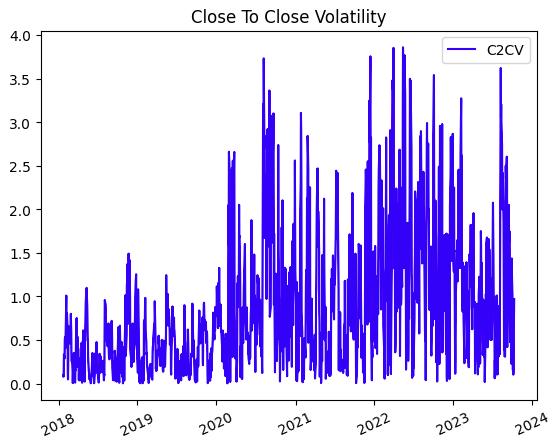
Y con esto ya podremos ver gráficamente el resultado de la volatilidad de Apple según esta fórmula:
Volatilidad de Yang Zhang
La Volatilidad de Yang Zhang es un indicador de volatilidad desarrollado por los científicos financieros Dennis Yang y Qiang Zhang y es especialmente útil para medir la volatilidad en mercados financieros caracterizados por patrones de precios asimétricos, como los mercados de opciones. En principio este indicador logra mejorar a otros muchos como el de Parkinson, ya que tiene en cuenta más factores (como el cambio entre los precios de Cierre y apertura) que lo hacen ser más fino.
Su fórmula es algo más complicada de las que hemos visto ahora:
Donde:
El código para poder llevar a cabo esto también es más complejo:
yang_zhang_volatility = []
for i in range(periodo, len(data)):
subset = data.iloc[i - periodo:i]
returns = subset['Close'].pct_change().dropna()
n = len(returns)
No = np.log(subset['Open'] ) - np.log( subset['Close'] )
Nu = np.log(subset['High'] ) - np.log(subset['Open'] )
Nd = np.log( subset['Low'] ) - np.log(subset['Open'] )
Nc = np.log( subset['Close'] ) - np.log(subset['Open'] )
Vrs = 1 / n * np.sum( Nu * ( Nu - Nc ) + Nd * ( Nd - Nc ))
Noavg = 1 / n * np.sum(No)
Vo = 1 / ( n - 1 ) * np.sum(( No - Noavg )**2 )
Ncavg = 1 / n * np.sum( Nc )
Vc = 1 / ( n - 1 ) * np.sum( ( Nc - Ncavg )**2 )
k = 0.34 / ( 1.34 + ( n + 1 ) / ( n - 1 ) )
Vyangzhang = Vo + k * Vc + ( 1 - k ) * Vrs
yang_zhang_volatility.append(Vyangzhang)
data['Yang_Zhang_Volatility'] = [np.nan] * periodo + yang_zhang_volatility
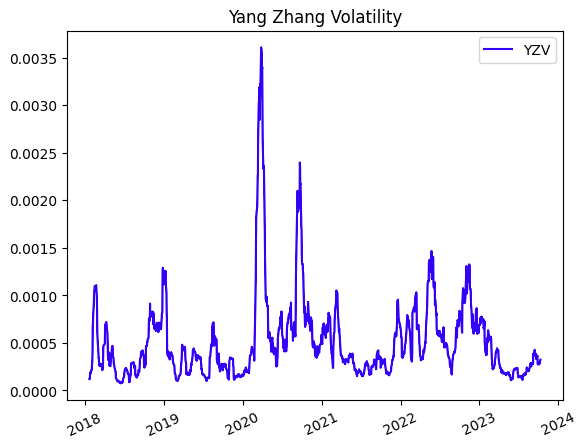
Y el resultado de la gráfica sería así:
Conclusión
Como hemos visto la forma de calcular la volatilidad de un activo es un tema muy amplio y muy complejo. Todavía nos hemos dejado muchas otras formas de calcular cuánto puede variar el precio de una acción en un determinado periodo de tiempo, pero como introducción a este tema no está mal este comienzo.
Aunque hemos visto varios indicadores y la lógica nos incita a coger el más complejo, no es siempre la mejor opción. Aunque el indicador con más elementos pueda ser el más fiable también tendrá el tiempo de ejecución más grande, y esto puede ser un problema en determinados entornos, en los que otros indicadores simples pueden ser suficientes. Así que también es algo a valorar.
Ahora ya podéis aplicar este tipo de indicador a vuestras operaciones de trading algorítmico, y tenerlo en cuenta para controlar grandes momentos de volatilidad. Ya es cosa vuestra si queréis hacer trading durante esos periodos o no, o incluso si queréis utilizarlo para intentar subiros a la cresta de alguna ola.
Como siempre, si tenéis cualquier duda o sugerencia de mejora del artículo no dudéis en poneros en contacto conmigo a través de nuestro formulario de contacto y os contestaré lo antes posible.
Un saludo,
Iván